Ever pondered the true nature of numbers, those fundamental building blocks of our universe? Today, we unravel a fascinating enigma: the square root of 66, exploring its properties, methods of calculation, and its surprising presence in both the abstract world of mathematics and the tangible realm of our daily lives.
The square root of 66, a value that represents a number which, when multiplied by itself, yields 66. This seemingly simple concept unlocks a world of mathematical exploration. We delve into how to find this value through various methods, ranging from approximations and the methodical approach of long division, to the elegance of prime factorization.
But what does it truly mean to "simplify" the square root of 66? It is not a perfect square, a number that results from squaring an integer. Therefore, its square root cannot be expressed as a whole number. To begin with, we understand that 66 is not a square number. Instead, it is a number with some intriguing characteristics. It is a triangular number, the sum of the natural numbers up to a certain point, and a hexagonal number, the number of dots needed to make a hexagon with a given side length. Furthermore, it is a palindrome number, reading the same forwards and backward.
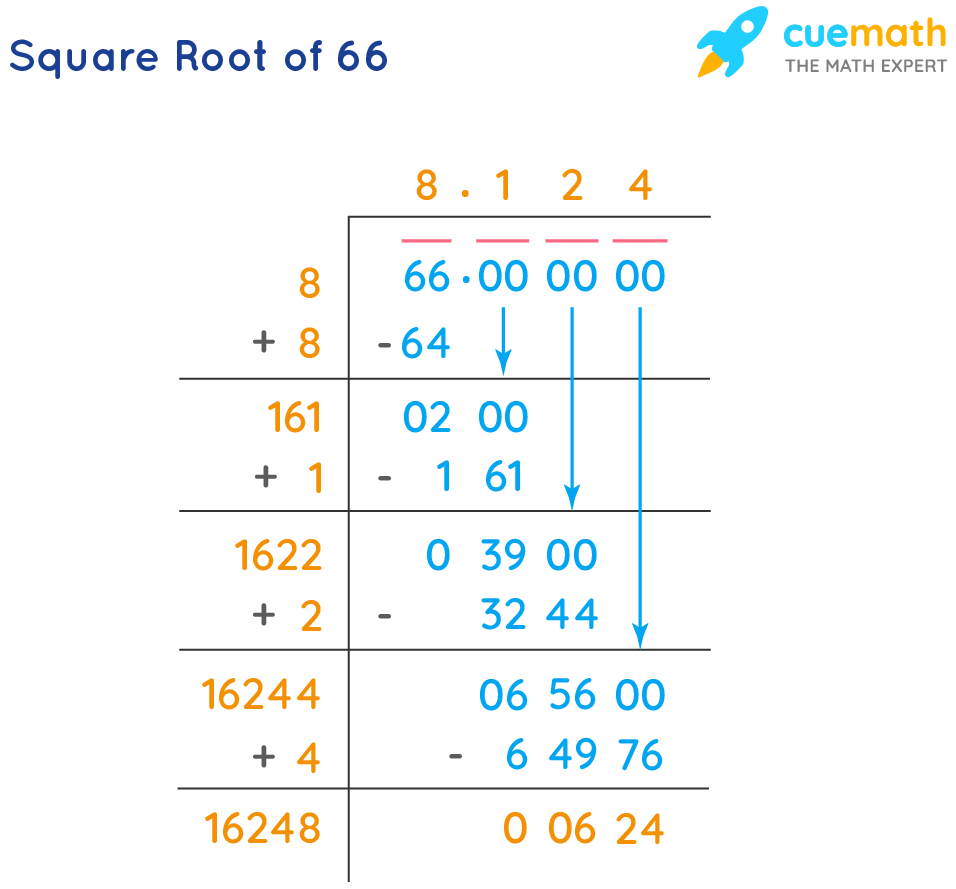
The value of the square root of 66 can be expressed in multiple forms. By definition, the square root of 66 is the value that, when multiplied by itself, equals 66. The square root of 66 is an irrational number, meaning it cannot be expressed as a simple fraction of two integers. Its decimal representation neither terminates nor repeats. In simpler terms, its decimal goes on forever without settling into a pattern. Through different approaches, the square root of 66 can be found. A straightforward method involves approximation. The square root of 66 is approximately 8.124. This result can be verified by multiplying 8.124 by itself, which gives a value close to 66. Another way is to use the square root calculator. These tools use algorithms to compute the square root efficiently and accurately. The long division method, a more traditional approach, can also be employed to determine the square root. This method requires a systematic process of dividing and estimating, resulting in the same approximation of 8.124.
| Characteristic | Description |
|---|---|
| Value | Approximately 8.12403840463596... (an irrational number) |
| Simplest Radical Form | 66 (cannot be simplified further) |
| Type | Irrational Number |
| Prime Factorization | 2 x 3 x 11 |
| Properties | 66 is a composite number. It is a triangular number, and a hexagonal number. |
| Methods of Calculation | Approximation, Long Division, Square Root Calculator, Babylonian Method. |
Let us consider how to calculate the square root of 66 with Excel or Google Sheets. By utilizing the `SQRT()` function, the square root of any number can be effortlessly determined. Therefore, `=SQRT(66)` entered into a cell will display the square root of 66. The function can also be incorporated into more complex formulas to perform calculations.
There are various methods to calculate the square root of a number, each with its own advantages. The long division method, though perhaps less common today due to the availability of calculators, offers a step-by-step process for finding the square root manually. The Babylonian method, also known as Heron's method, is an iterative approach that provides increasingly accurate approximations of the square root. Modern calculators and software use algorithms to efficiently and accurately compute square roots, offering a quick and easy solution.
How does one put this knowledge to practical use? The concept of a square root is fundamental across several areas of mathematics, including algebra, geometry, and trigonometry. In geometry, the square root is essential when determining the side lengths of squares, and the properties of various geometric shapes. In real life, the square root has several useful applications. Calculating the area of a square, understanding the spread of a circular object or the calculation of the lengths of the sides of a right triangle. It is also applied in engineering, physics, and finance. For instance, in engineering, the square root may be employed in calculating the natural frequency of a vibrating system.
It's worth remembering that the square root of 66 is an irrational number. Irrational numbers have decimal representations that neither terminate nor repeat. Its value goes on forever, without settling into a pattern. For practical purposes, we often work with approximations, such as 8.124. The square root can be used in various calculations and fields.
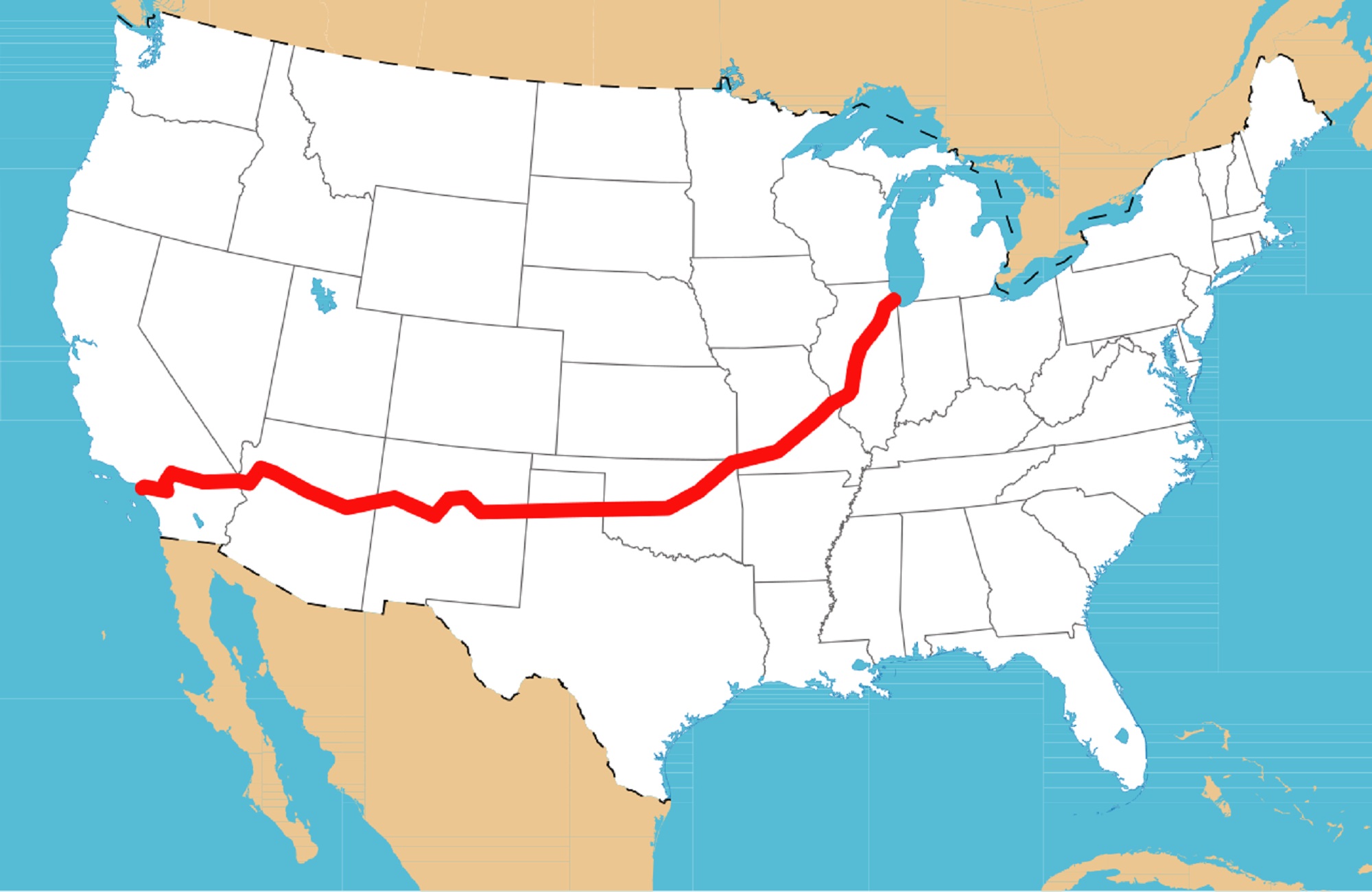
Beyond the realm of abstract calculations, the number 66 and its square root have associations with other elements of the world. Route 66, also known as the Mother Road or the Will Rogers Highway, stands as a testament to the spirit of American adventure. It was one of the original highways in the United States, established on November 11, 1926. This iconic route, which originally spanned from Chicago, Illinois, to Santa Monica, California, is a cultural symbol. The road underwent many improvements and realignments during its lifetime. The federal highway act of 1956 sounded the death knell for the old road, and gradually segments were replaced with new, safer and faster superhighways.
In the city of St. Louis, Missouri, "Root 66" is the name of medical marijuana dispensaries. The "Root 66" dispensaries in St. Louis, Missouri, pay homage to the famous route, which itself traversed through parts of Missouri. The name is a clever pun, combining the mathematical concept of a "root" with the famous highway. These establishments can be found in locations such as South Grand, Dogtown, and St. Peters. Our wentzville root 66 store is located in the fastest growing city in the state of missouri.
The applications of square roots extend far beyond the academic context, impacting fields such as engineering, physics, and finance. For example, in engineering, the concept can be applied to determine the natural frequency of a vibrating system. Furthermore, in fields like finance, it plays a role in the calculation of compound interest and other financial models. In a world increasingly reliant on technology, understanding the square root and its associated concepts remains a crucial skill.
The essence of the square root is about understanding numbers. Each of these methods, whether long division or using a calculator, is a journey into the heart of numerical analysis. From the precision of mathematical formulas to the cultural significance of iconic routes, the square root of 66 weaves its way into the fabric of our world.